Publication Number: EBAE 161-92
Last Electronic Revision: March 1996 (JWM)
A hydraulic ram (or water ram) pump is a simple, motorless device for pumping water at low flow rates. It uses the energy of flowing water to lift water from a stream, pond, or spring to an elevated storage tank or to a discharge point. It is suitable for use where small quantities of water are required and power supplies are limited, such as for household, garden, or livestock water supply. A hydraulic ram pump is useful where the water source flows constantly and the usable fall from the water source to the pump location is at least 3 feet.
Principles of Operation
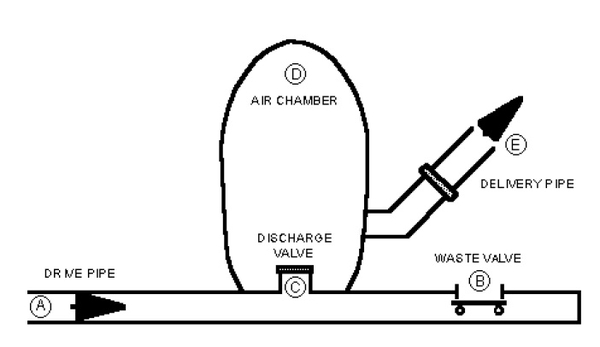
Components of a hydraulic ram pump are illustrated in Figure 1. Its operation is based on converting the velocity energy in flowing water into elevation lift. Water flows from the source through the drive pipe (A) and escapes through the waste valve (B) until it builds enough pressure to suddenly close the waste valve. Water then surges through the interior discharge valve (C) into the air chamber (D), compressing air trapped in the chamber. When the pressurized water reaches equilibrium with the trapped air, it rebounds, causing the discharge valve (C) to close. Pressurized water then escapes from the air chamber through a check valve and up the delivery pipe (E) to its destination. The closing of the discharge valve (C) causes a slight vacuum, allowing the waste valve (B) to open again, initiating a new cycle.
The cycle repeats between 20 and 100 times per minute, depending upon the flow rate. If properly installed, a hydraulic ram will operate continuously with a minimum of attention as long as the flowing water supply is continuous and excess water is drained away from the pump.
System Design
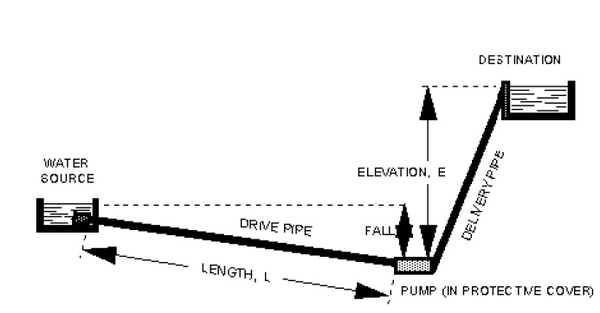
A typical hydraulic ram pump system layout is illustrated in Figure 2. Each of the following must be considered when designing a hydraulic ram pump system:
- available water source
- length and fall of the drive pipe for channeling water from the source to the pump
- size of the hydraulic ram pump
- elevation lift from the pump to the destination
- desired pumping flow rate through the delivery pipe to the destination.
A hydraulic ram pump system is designed to deliver the desired pumping flow rate for a given elevation lift. The range of available flow rates and elevation lifts is related to the flow quantity and velocity from the water source through the drive pipe. The mathematical relationship for pumping flow rate is based upon the flow rate through the drive pipe, the vertical fall from the source through the drive pipe, and the vertical elevation lift from the pump to the point of use. These variables are illustrated in Figure 2.
Equation 1 is used to calculate pumping rate:
\(\mathrm{Q}=\ 1440\times\left[\frac{\mathrm{E}\times\mathrm{S}}{\left(\mathrm{L}/\mathrm{F}\right)}\right]\)
where:
Q=pumping rate in gallons per day (gpd)
E=efficiency of a hydraulic ram pump installation, typically equal to 0.6
S=source flow rate through the drive pipe in gallons per minute (gpm)
L=vertical elevation lift from the pump to the destination in feet F=vertical fall from the source through the drive pipe in feet.
To convert the pumping rate expressed in gallons per day(gpd) to gallons per minute(gpm), dividen by 1440. The following example illustrates an application of Equation 1.
Example.
A hydraulic ram will be used to pump water from a stream with an average flow rate of 20 gpm up to a water tank located 24 feet vertically above the pump. The vertical fall through the drive pipe in the stream to the pump is 4 feet. Assume a pumping efficiency of 0.6. What is the maximum pumping rate from the hydraulic ram pump?
In this example, E = 0.6, S = 20 gpm, L = 24 feet, and F = 4 feet. The resulting pumping rate, Q, is calculated as:
\(\mathrm{Q}=\ 1440\times\left[\frac{0.6\times20}{\left(\mathrm{24}/\mathrm{4}\right)}\right]=2880\ \mathrm{gpd}\)
The maximum pumping rate delivered by the hydraulic ram pump operating under these conditions is 2880 gallons per day, or 2 gallons per minute.
The example shows how the pumping rate, Q, is directly related to the source flow rate, S. If S were to double from 20 gpm to 40 gpm, the resulting pumping rate would also double to 5760 gpd, or 4 gpm.
The example also shows how the pumping rate, Q, is inversely related to the ratio of vertical elevation lift to vertical fall, L/F. If L were to double from 24 feet to 48 feet, the lift to fall ratio, L/F, would double from 6 to 12. The resulting pumping rate would decrease by half to 1440 gpd, or 1 gpm.
Table 1. Maximum pumping rates for a range of source flow rates and lift to fall ratios assuming a pumping efficiency of 0.6.
|
Lift to Fall Ratio L/F (ft/ft) |
Maximum Pumping Rate, Q (gpd) | |||||||
| Source Flow Rate, S (gpm) | ||||||||
| 2 | 5 | 10 | 15 | 20 | 30 | 50 | 100 | |
| 2 | 864 | 2,160 | 4,320 | 6,480 | 8,640 | 12,960 | 21,600 | 43,200 |
| 3 | 576 | 1,440 | 2,880 | 4,320 | 5,760 | 8,640 | 14,400 | 28,800 |
| 4 | 432 | 1,080 | 2,160 | 3,240 | 4,320 | 6,480 | 10,800 | 21,600 |
| 5 | 346 | 864 | 1,728 | 2,592 | 3,456 | 5,184 | 8,640 | 17,280 |
| 6 | 288 | 720 | 1,440 | 2,160 | 2,880 | 4,320 | 7,200 | 14,400 |
| 7 | 247 | 617 | 1,234 | 1,851 | 2,469 | 3,703 | 6,171 | 12,343 |
| 8 | 216 | 540 | 1,080 | 1,620 | 2,160 | 3,240 | 5,400 | 10,800 |
| 9 | 192 | 480 | 960 | 1,440 | 1,920 | 2,880 | 4,800 | 9,600 |
| 10 | 173 | 432 | 864 | 1,296 | 1,728 | 2,592 | 4,320 | 8,640 |
| 12 | 144 | 360 | 720 | 1,080 | 1,440 | 2,160 | 3,600 | 7,200 |
| 14 | 123 | 309 | 617 | 926 | 1,234 | 1,851 | 3,086 | 6,171 |
| 16 | 108 | 270 | 540 | 810 | 1,080 | 1,620 | 2,700 | 5,400 |
| 18 | 96 | 240 | 480 | 720 | 960 | 1,440 | 2,400 | 4,800 |
| 20 | 86 | 216 | 432 | 648 | 864 | 1,296 | 2,160 | 4,320 |
| 25 | 69 | 173 | 346 | 518 | 691 | 1,037 | 1,728 | 3,456 |
| 30 | 58 | 144 | 288 | 432 | 576 | 864 | 1,440 | 2,880 |
| 35 | 49 | 123 | 247 | 370 | 494 | 741 | 1,234 | 2,469 |
| 40 | 43 | 108 | 216 | 324 | 432 | 648 | 1,080 | 2,160 |
| 45 | 38 | 96 | 192 | 288 | 384 | 576 | 960 | 1,920 |
| 50 | 35 | 86 | 173 | 259 | 346 | 518 | 864 | 1,728 |
| 60 | 29 | 72 | 144 | 216 | 288 | 432 | 720 | 1,440 |
| 70 | 25 | 62 | 123 | 185 | 247 | 370 | 617 | 1,234 |
| 80 | 22 | 54 | 108 | 162 | 216 | 324 | 540 | 1,080 |
| 90 | 19 | 48 | 96 | 144 | 192 | 288 | 480 | 960 |
| 100 | 17 | 43 | 86 | 130 | 173 | 259 | 432 | 864 |
Table 1 lists maximum pumping rates, Q, for a range of source flow rates, S, and lift to fall ratios, L/F, calculated using Equation 1 with an assumed pumping efficiency, E, of 0.6. To illustrate the use of Table 1, consider a hydraulic ram system with S = 30 gpm, L = 150 feet, and F = 5 feet. The calculated lift to fall ratio, L/F, is 30. The resulting value for Q is 864 gpd, or 0.6 gpm.
Hydraulic ram pumps are sized based upon drive pipe diameter. The size of drive pipe selected depends upon the available source water flow rate. All makes of pumps built for a given size drive pipe use about the same source flow rate. Available sizes range from 3/4-inch to 6-inch diameters, with drive pipe water flow requirements of 2 to 150 gpm. Hydraulic ram pumps typically can pump up to a maximum of 50 gpm (72,000 gpd) with maximum elevation lifts of up to 400 feet.
Approximate characteristics of hydraulic ram pumps for use in selecting pumps are listed in Table 2. The recommended delivery pipe diameter is normally half the drive pipe diameter. For the system described in the example above, the available source water flow rate is 10 gpm. From Table 2, a pump with a 1-inch drive pipe diameter and a 1/2-inch delivery pipe diameter is selected for this system.
Installation
The location of the water source in relation to the desired point of water use determines how the hydraulic ram pump will be installed. The length of drive pipe should be at least 5 times the vertical fall to ensure proper operation. The length of delivery pipe is not usually considered important because friction losses in the delivery pipe are normally small due to low flow rates. For very long delivery pipes or high flow rates, friction losses will have an impact on the performance of the hydraulic ram pump. The diameter of the delivery pipe should never be reduced below that recommended by the manufacturer.
To measure the available source water flow rate from a spring or stream, build a small earthen dam with an outlet pipe for water to run through. Place a large bucket or barrel of known volume below the outlet pipe, and measure the number of seconds it takes to fill the container. Then calculate the number of gallons per minute flowing through the outlet. For example, if it takes 30 seconds to fill a 5-gallon bucket, the available source water flow rate is 10 gpm. The lowest flow rates are typically in the summer months. Measure the flow rate during this period to ensure that the year-round capacity of the system is adequate.
Purchasing a System
Prices for hydraulic ram pumps range from several hundred to several thousand dollars depending on size and performance characteristics. Contact manufacturers to determine prices and ordering specifications. Send the information listed in Table 3 to the manufacturer to assist in sizing your system properly.
Acknowledgments
This fact sheet adapted from materials prepared by the California, Florida, and South Carolina Cooperative Extension Services.
Publication date: March 1, 1996
Reviewed/Revised: Dec. 11, 2024
N.C. Cooperative Extension prohibits discrimination and harassment regardless of age, color, disability, family and marital status, gender identity, national origin, political beliefs, race, religion, sex (including pregnancy), sexual orientation and veteran status.